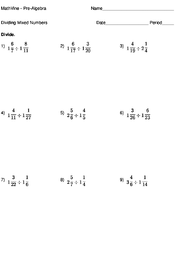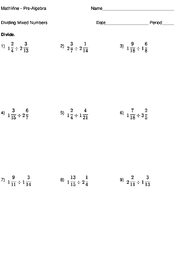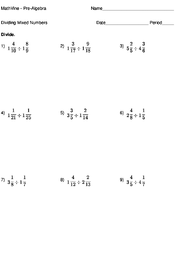Home > Pre-Algebra > Fractions > Dividing Mixed Numbers
Dividing Mixed Numbers
Introduction
In order to divide mixed fractions, we must first convert the mixed fraction to an improper fraction. Then we proceed with the calculation for dividing fractions (i.e. multiplying one fraction by the reciprocal of the other).
Terms
Fraction - Fractions are used when using numbers to express parts of whole.
Mixed Fraction - A fraction where a whole number is combined with a fraction.
Improper Fraction - A fraction where the numerator is greater than the denominator.
Reciprocal - The reciprocal of a fraction is the fraction turned upside down.
Lesson
If we are given the following problem: , we must first convert both fractions to improper fractions. 1 ½ = 3/2 and 3 ½ = 7/2. We then multiply the first fraction with the reciprocal of the second – which can be reduced to 3/7. If we are given one whole number and one mixed fraction, the procedure is similar. can be written as . We multiply 20 by the reciprocal .
Examples
Dividing Mixed Numbers (Example #1)
Convert the mixed numbers to improper fractions
To divide by , multiply by
Dividing Mixed Numbers (Example #2)
Convert the mixed numbers to improper fractions
To divide by , multiply by
Dividing Mixed Numbers (Example #3)
Convert the mixed numbers to improper fractions
To divide by , multiply by
Dividing Mixed Numbers (Example #4)
Convert the mixed numbers to improper fractions
To divide by , multiply by