Area of a Triangle Lesson

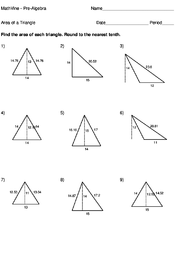
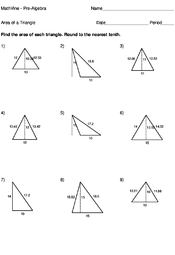
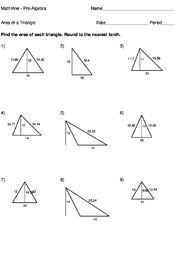
Home > Pre-Algebra > Area > Area of a Triangle Lesson

Area of a Triangle Lesson

Introduction

A triangle is a three-sided polygon. Triangles are one of the most basic geometric shapes, and their properties can be used to determine the area of many other polygons. A right triangle is a triangle which has one 90 degree angle between sides. An equilateral triangle is a triangle which has three sides of equal length with equal angles between them. An Isosceles triangle is a triangle which has two equal sides and two equal angles.

Terms

Area - A quantity that expresses the extent of a two-dimensional shape.

Triangle - A polygon with three sides.

Polygon - A plane figure with at least three sides.

Right Triangle - A triangle where one angle is a right angle (90 degrees).

Isoceles Triangle - A triangle with two equal sides.

Equilateral Triangle - A triangle with three equal sides.

Lesson

The formula for the area of a triangle is:

$ext{Area} = dfrac{a*h}{2}$

where a is the length of the base, and h is the height. You can think of the area of a triangle as being half of the area of a rectangle with sides a and h.

If a rectangle has a base of length 3 and height of 4, for example, the area is

$ext{Area} = dfrac{a*h}{2}$

$ext{Area} = dfrac{3*4}{2}$

$ext{Area} = dfrac{12}{2}$

$ext{Area} = 6$

Examples

Area of a Triangle

\text{Area} = \dfrac{1}{2} * \text{Base} * \text{Height}

\text{Area} = \dfrac{1}{2} * 15 * 10

\text{Area} = 75

Area of a Triangle (w/ Decimals)

\text{Area} = \dfrac{1}{2} * \text{Base} * \text{Height}

\text{Area} = \dfrac{1}{2} * 13.5 * 8.4

\text{Area} = 56.7