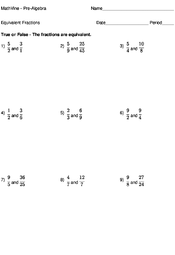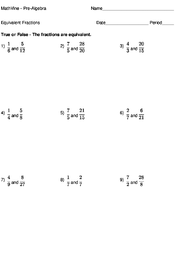Equivalent Fractions

Home > Pre-Algebra > Fractions > Equivalent Fractions

Introduction

Equivalent fractions are fractions that are equal. In order to determine if one fraction is equal or equivalent to another, both fractions must first be simplified if needed.

Terms

- Fractions are used when using numbers to express parts of whole.

- a fraction expressed in its lowest terms.

Lesson

To determine if a fraction is equivalent to another, we need to compare the two fractions in their simplest form. So if we are given $rac{1}{4}$ and $rac{2}{8}$ , we can see that $rac{1}{4}$ is in its simplest form, but $rac{2}{8}$ can be further reduced to $rac{1}{4}$ by dividing the top and bottom by 2.

$dfrac{2}{8} div dfrac{2}{2} = dfrac{1}{4}$

Therefore $rac{1}{4}$ and $rac{2}{8}$ are equivalent fractions.

Similarly, if we are given $rac{5}{10}$ and $rac{21}{30}$ , we first simplify both fractions.

$dfrac{5}{10} div dfrac{5}{5} = dfrac{1}{2}$

$dfrac{21}{30} div dfrac{3}{3} = dfrac{7}{10}$

We can now see that $rac{5}{10}$ is NOT equivalent to $rac{21}{30}$ , because $rac{1}{2}$ is not equivalent to $rac{7}{10}$

To find the equivalent of a fraction when we are given either the numerator or denominator is similar to expressing a fraction in higher terms. If we are told to solve the following problem:

$dfrac{3}{10} = dfrac{15}{?}$

we can determine that in order for the new numerator to equal 15, the original numerator must be multiplied by 5. So we multiply the denominator by 5 as well, and get the answer

$dfrac{3}{10} = dfrac{15}{50}$

Examples

Equivalent Fractions (Example #1)

\dfrac{8}{5}

and

\dfrac{16}{10}

First, write each fraction in lowest terms

The greatest common divisor of

8

and

5

is 1, so

\dfrac{8}{5}

is already in lowest terms

\dfrac{16}{10}

can be reduced, since

2

is a factor of both

16

and

10

\dfrac{16}{10} \div \dfrac{2}{2} = \dfrac{8}{5}

The fraction is now in lowest terms

\dfrac{8}{5}

is equal to

\dfrac{16}{10}

Make Equivalent Fraction (Example #1)

\dfrac{\text{6}}{\text{5}} = \dfrac{\text{3}}{\text{x}}

We have to multiply the first numerator (6) by 0 to get the second numerator (3)

To make an equivalent fraction, we need to multiply the denominator by 0 as well

Equivalent Fractions (Example #2)

\dfrac{3}{4}

and

\dfrac{5}{8}

First, write each fraction in lowest terms

The greatest common divisor of

3

and

4

is 1, so

\dfrac{3}{4}

is already in lowest terms

The greatest common divisor of

5

and

8

is 1, so

\dfrac{5}{8}

is already in lowest terms

\dfrac{3}{4}

is not equal to

\dfrac{5}{8}

Make Equivalent Fraction (Example #2)

\dfrac{\text{3}}{\text{4}} = \dfrac{\text{3}}{\text{x}}

We have to multiply the first numerator (3) by 1 to get the second numerator (3)

To make an equivalent fraction, we need to multiply the denominator by 1 as well