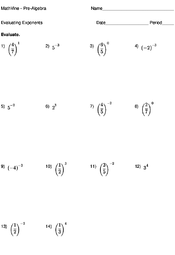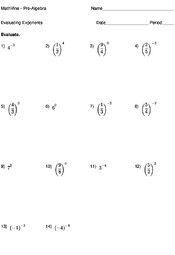Evaluating Exponents
Introduction
Exponents are a way of writing that a number is being multiplied by itself and telling you how many times to do it.
For example, if we multiply 3 x 3, we can write . The tells us that you have 2 threes that you are multiplying together. If we were to have then we would have three threes to multiply together which would be 3 x 3 x 3.
Terms
Lesson
To evaluate an exponent you need to break it up into its parts. The first number tells you what you are multiplying, and the exponent tells you how many of these numbers to multiply together. For example, in the expression:
The 5 is the number to be multiplied, and the tells us that we need to multiply together two fives, so
= 5 x 5 = 25
In the expression:
The 2 is the number to be multiplied, and we need to do it 6 times:
= 2 x 2 x 2 x 2 x 2 x 2 = 64
Some rules to remember:
Any exponent of 0 is still zero.
= 0 x 0 x 0 = 0
Any exponent of 1 is still 1.
= 1 x 1 x 1 x 1 x 1 = 1
Any number to the exponent of 0 = 1
= 1
= 1
= 1