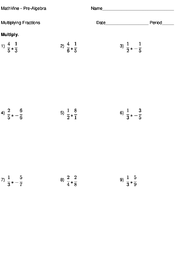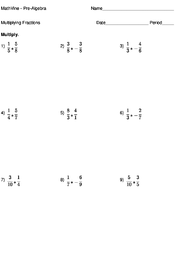Multiplying Fractions

Home > Pre-Algebra > Fractions > Multiplying Fractions

Introduction

Multiplying fractions is as simple as multiplying the numerators together, and then multiplying the denominators together. Note: Improper fractions are multiplied in the same way.

Terms

Fractions - Fractions are used when using numbers to express parts of whole.

Lesson

When given two or more fractions to multiply together, we first multiply all the numerators – this becomes the numerator of the answer. We can then multiply the denominators together to get the denominator of the answer. So if we are given $dfrac{1}{5} * dfrac{7}{8}$ the numerators are multiplied ( $1*7=7$ ) and the denominators are multiplied ( $5*8 = 40$ ) giving as $rac{7}{40}$ as the answer.

Here is another example:

$dfrac{2}{3} * dfrac{4}{9} = dfrac{2*4}{3*9} = dfrac{8}{27}$

Examples

Multiplying Fractions (Example #1)

\dfrac{2}{5} * \dfrac{1}{5}

\dfrac{(2 * 1)}{(5 * 5)}

\dfrac{2}{25}

Multiplying Fractions (Example #2)

\dfrac{3}{4} * \dfrac{4}{5}

\dfrac{(3 * 4)}{(4 * 5)}

\dfrac{(3 * 4^1)}{(4^1 * 5)}

\dfrac{3}{5}

Multiplying Fractions (Example #3)

\dfrac{9}{10} * \dfrac{4}{5}

\dfrac{(9 * 4)}{(10 * 5)}

\dfrac{(9 * 4^2)}{(10^5 * 5)}

\dfrac{18}{25}

Multiplying Fractions (Example #4)

\dfrac{1}{2} * \dfrac{1}{4}

\dfrac{(1 * 1)}{(2 * 4)}

\dfrac{1}{8}