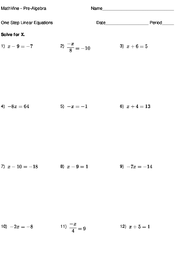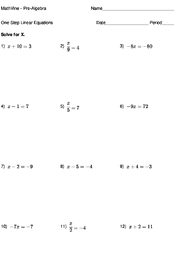One Step Linear Equations
Introduction
A linear equation is an equation describing a line on a graph. The usual format for a linear equation is y=mx+b (this is called the slope-intercept format). m is the slope of the line (how steeply it goes up or down) and b is the y-intercept (which is where the line crosses the y-axis - also the point at which x=0).
To solve one-step linear equations, you just have to combine the like terms.
Terms
Lesson
For this type of linear equation, we'll be focusing on the slope-intercept format (y=mx+b).
That means we need to get y on one side of the equation (not 2y, or -y, but exactly y), and the x variable and the number on the right-hand side of the equation.
An example of a slope-intercept linear equation is:
To 'solve' a linear equation, we don't find the value for x and y (and we can't, unless we're given another line to combine it with), but instead, we have to put the equation in this format.
If we are given the equation:
Since the right-hand side of the equation is complete, we just need to combine the like terms on the left-hand side. To do that, we do 7y-6y, which gives the answer y.
Therefore, the solution is:
We can solve the equation in one step as long as there is only one set of like terms to combine.