How to Find the Area of a Circle
Introduction
A circle is a geometric figure which is the set of all points in a plane that are equidistant from a given point called its center.
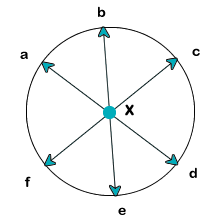
The distance between any point of the circle and the center is called the radius. The distance from one side of the circle to another that passes through the center is called the diameter. The diameter is always twice as long as the radius.
Terms
Lesson
Area of a Circle Formula:
If the radius is given as 4, we can substitute it into the equation above like this:
If we are given a diameter of 10 instead of the radius, we need to calculate the radius before we can use the formula. We know that the radius is always half the diameter (), so we can plug in 10 as the diameter and calculate the radius:
Then we are able to use the formula above: