Perimeter of a Rectangle

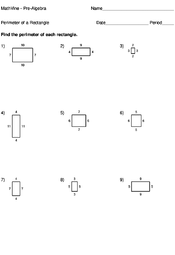
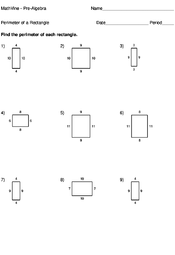
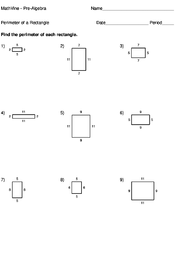
Home > Pre-Algebra > Perimeter > Perimeter of a Rectangle

Perimeter of a Rectangle

Introduction

The perimeter of a rectangle can be described as the distance around all four sides of the rectangle. The green box around the rectangle below indicates the perimeter of the rectangle.

Terms

Rectangle - A polygon with four straight sides and four right angles, esp one with unequal adjacent sides.

Perimeter - The distance around all the edges of a geometric figure.

Lesson

Calculating the perimeter of a rectangle is as easy as simply adding the lengths of all the sides together. The formula for this calculation is:

Perimeter of a Rectangle Formula

$Perimeter = 2*b + 2*h$

where ‘b’ is the base length, and ‘h’ is the height

So for a rectangle with a base of 5 and a height of 2, the perimeter would be: $5 + 5 + 2 + 2 =$

$2*5 + 2*2 =$

$10 + 4 = 14$

Examples

Perimeter of a Rectangle (Example #1)

Perimeter = 2 * Length + 2 * Width

Perimeter = 2 *

9

+ 2 *

12

\text{Perimeter} = 18 + 24

\text{Perimeter} = 42

Perimeter of a Rectangle (Example #2)

Perimeter = 2 * Length + 2 * Width

Perimeter = 2 *

8

+ 2 *

13

\text{Perimeter} = 16 + 26

\text{Perimeter} = 42

Perimeter of a Rectangle (Example #3)

Perimeter = 2 * Length + 2 * Width

Perimeter = 2 *

15

+ 2 *

12.5

\text{Perimeter} = 30 + 25

\text{Perimeter} = 55

Perimeter of a Rectangle (Example #4)

Perimeter = 2 * Length + 2 * Width

Perimeter = 2 *

14.9

+ 2 *

10.1

\text{Perimeter} = 29.8 + 20.2

\text{Perimeter} = 50